
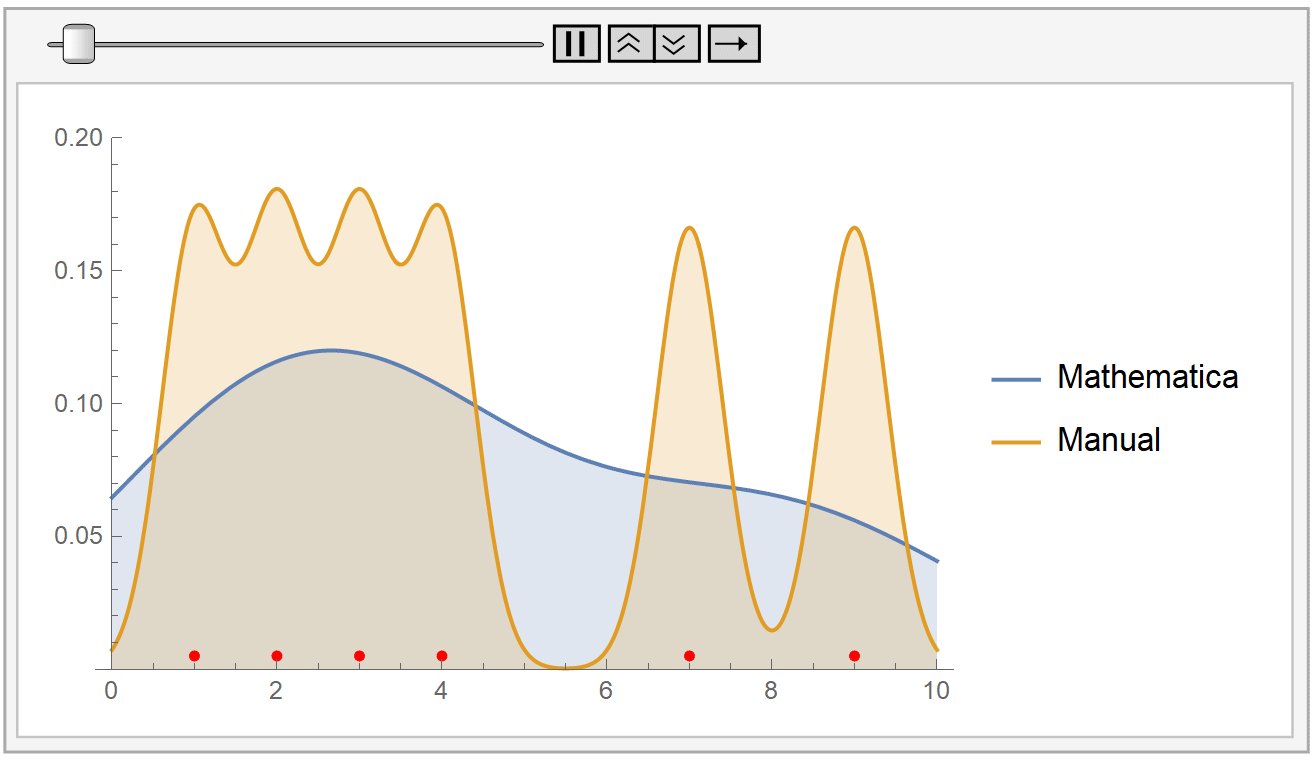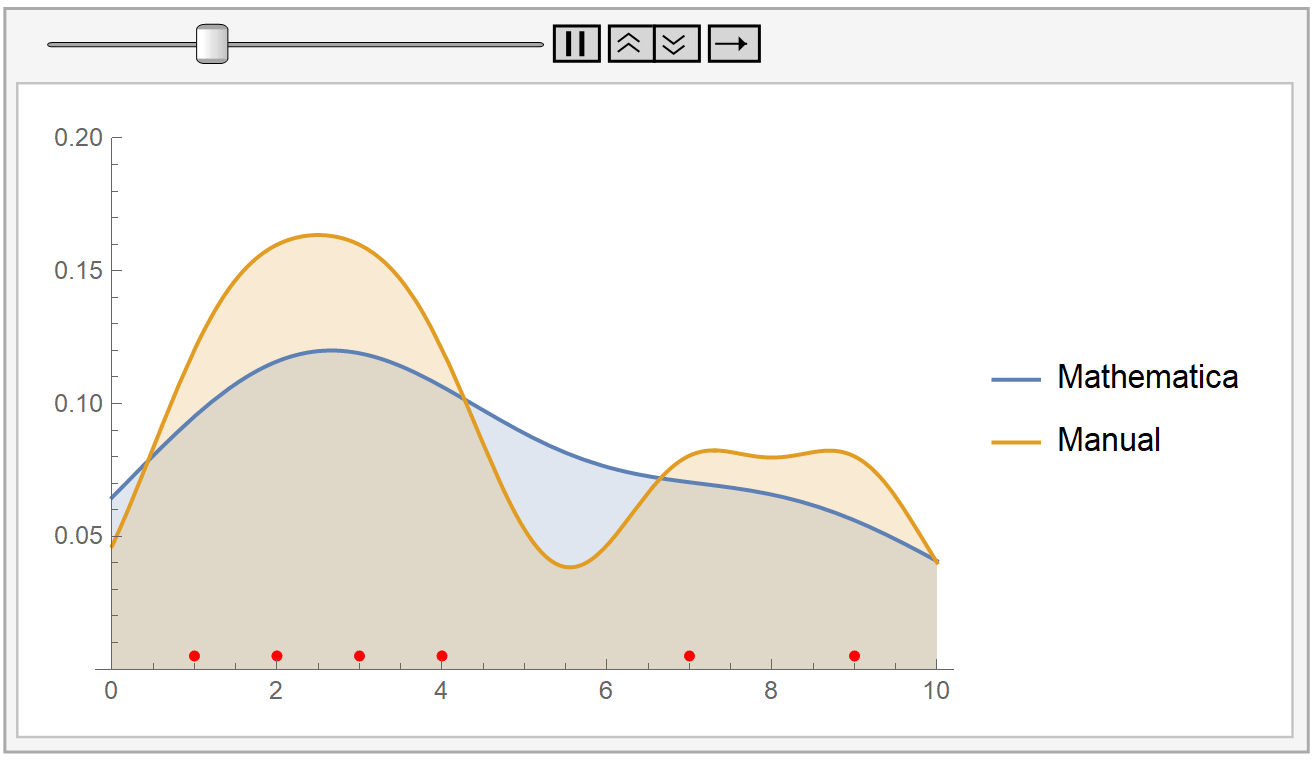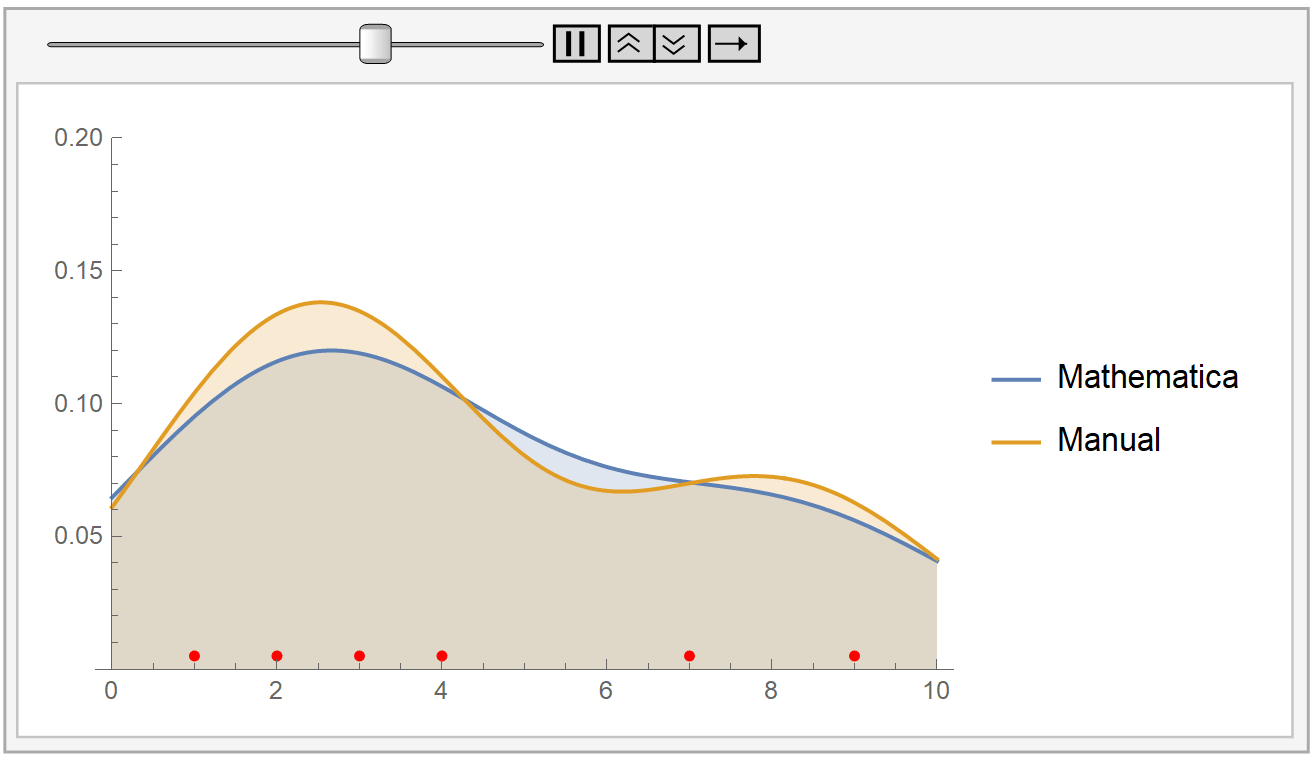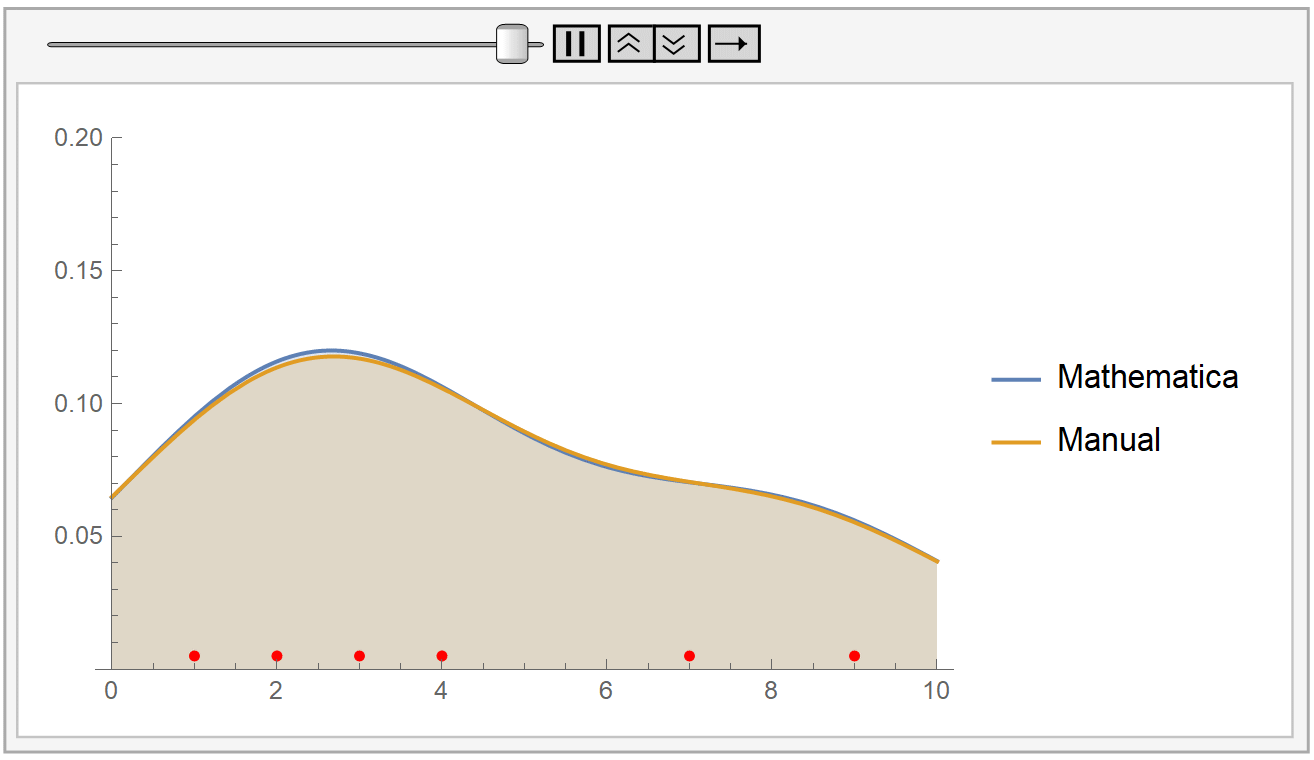
We instantiate our framework with the Laplacian and Exponential kernels, two popular kernels which possess the aforementioned property. In this work, we present an improvement to their framework that retains the same query time, while requiring only linear space and linear preprocessing time. These limitations inhibit the practical applicability of their approach on large datasets. This method achieves robustness by combining a traditional kernel density estimator (KDE) with ideas from classical M-estimation. However, their data structure requires a significantly increased super-linear storage space, as well as super-linear preprocessing time. Adaptive kernel density estimator is an efficient estimator when the density to be estimated has long tail or multi-mode. Recently, Charikar and Siminelakis (2017) presented a framework for kernel density estimation in provably sublinear query time, for kernels that possess a certain hashing-based property.
#Kernel density estimation generator#
As a counterpart it entails more computational burden when the random generator of the null hypothesis density function is not available in R and random.function must be used.AuthorFeedback Bibtex MetaReview Metadata Paper Reviews SupplementalĪrturs Backurs, Piotr Indyk, Tal Wagner Abstract Kernel density estimation is a non-parametric model also know as KDE, it’s a technique that lets you create a smooth curve given a set of data. The first diagram shows a set of 5 events (observed values) marked by crosses. This idea is simplest to understand by looking at the example in the diagrams below.
#Kernel density estimation windows#
It is also referred to by its traditional name, the Parzen-Rosenblatt Window method, after its discoverers. This chapter describes the kernel density estimation technique that can be considered a smoothed version of the Parzen windows presented in the Chapter 2. In light of the simulation results, we can conclude that (i) the tests implemented in the truncgof package should not be used to assess goodness-of-fit (at least for non-truncated distributions), (ii) the test fan.test shows an over-tendency to not reject the null hypothesis, being visibly miscalibrated (at least in its default option, where the bandwidth parameter is estimated using dpik from package KernSmooth), (iii) the tests ks.test and ad.test show similar power, with ad.test being slightly preferable in large samples, and (iv) dgeometric.test represents a good alternative given its satisfactory calibration and its, in general, superior power in samples of medium and large sizes. Kernel density estimation (KDE) is a procedure that provides an alternative to the use of histograms as a means of generating frequency distributions. Kernel density estimation (KDE) is a non-parametric method for estimating the probability density function of a given random variable. In addition to dgeometric.test and fan.test, the GoFKernel package adds a couple of functions that R users might also find of interest: density.reflected extends density, allowing the computation of consistent kernel density estimates for bounded random variables, and random.function offers an ad-hoc and universal (although computational expensive and potentially inaccurate for long tail distributions) sampling method. This paper (i) proposes dgeometric.test, a new implementation of the test that measures the discrepancy between a sample kernel estimate of the density function and the null hypothesis density function on the L1 -norm, (ii) introduces the GoFKernel package, and (iii) performs a large simulation exercise to assess the calibration and sensitivity of the above listed tests as well as the Fan's test (Fan 1994), fan.test, also implemented in the GoFKernel package. Indeed, as far as I know, almost all the tests currently available in R related to this issue (ks.test in package stats, ad.test in package ADGofTest, and ad.test, ad2.test, ks.test, v.test and w2.test in package truncgof) use one of these two distances on cumulative distribution functions. To assess the goodness-of-fit of a sample to a continuous random distribution, the most popular approach has been based on measuring, using either L∞ - or L2 -norms, the distance between the null hypothesis cumulative distribution function and the empirical cumulative distribution function.


 0 kommentar(er)
0 kommentar(er)
